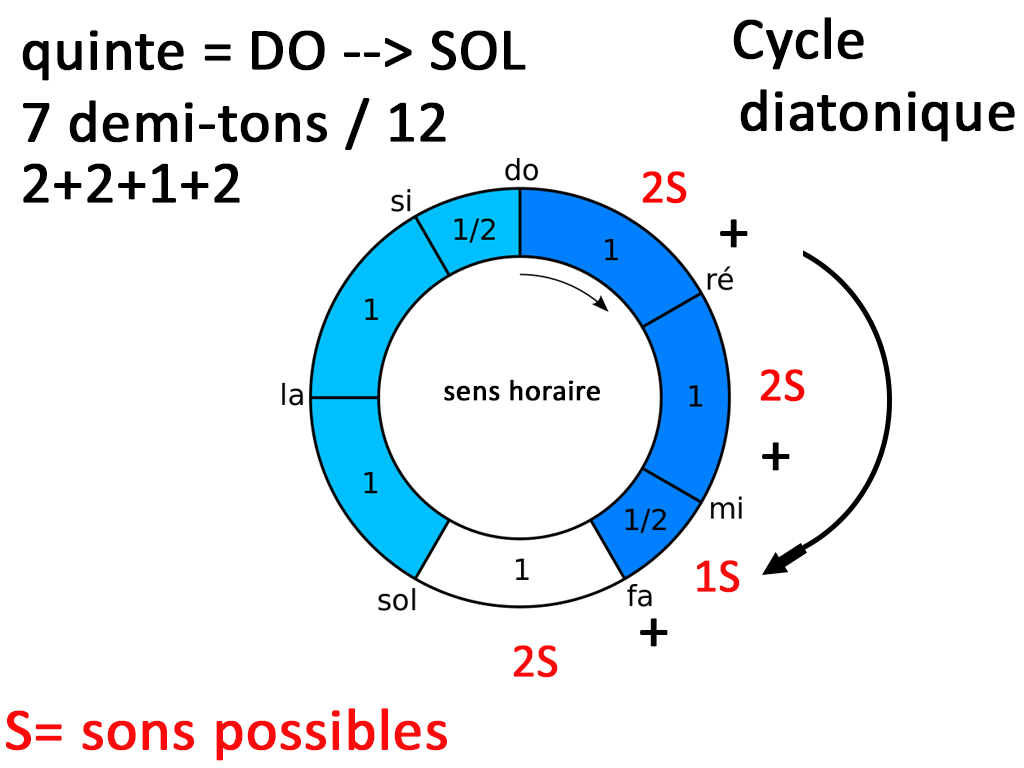
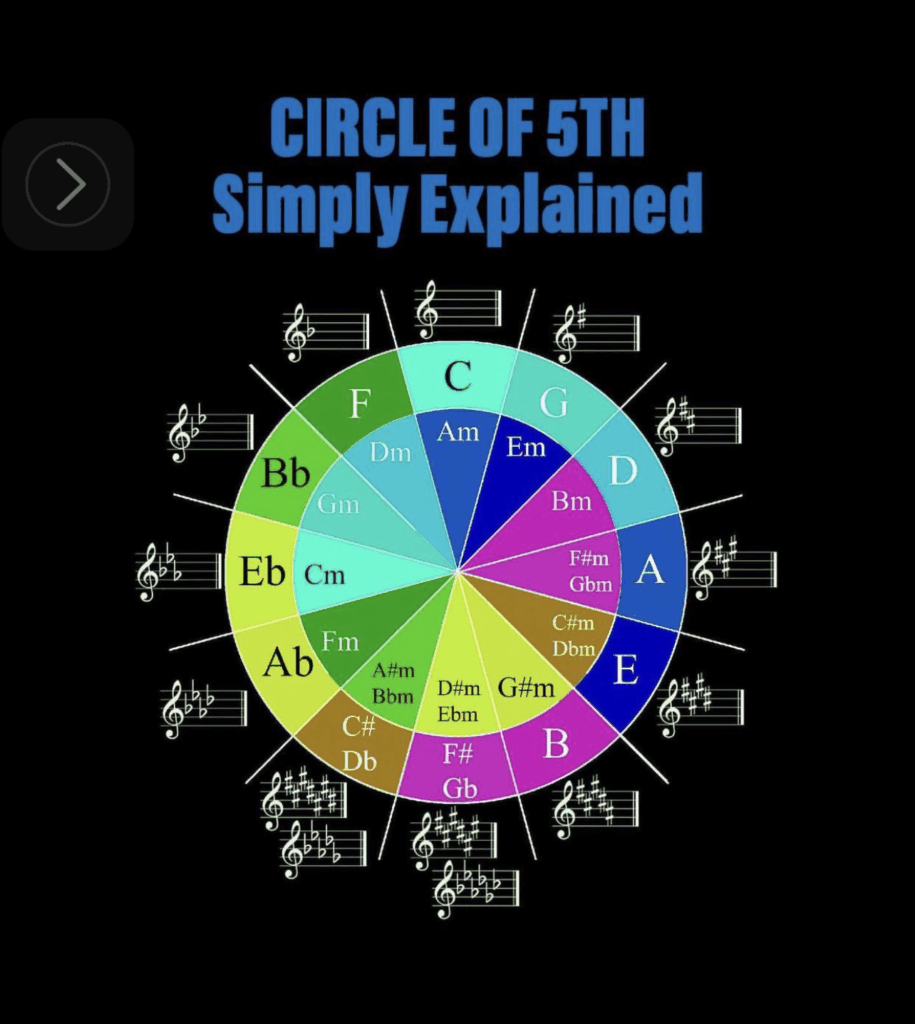
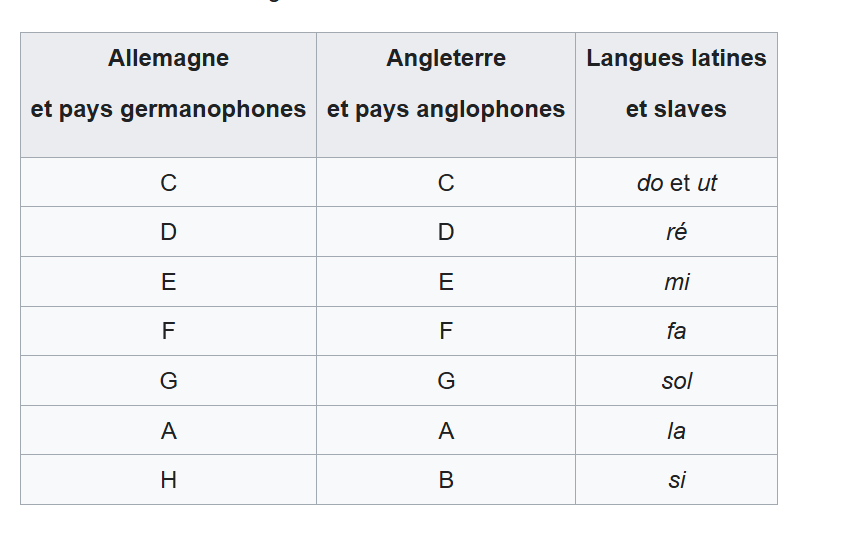
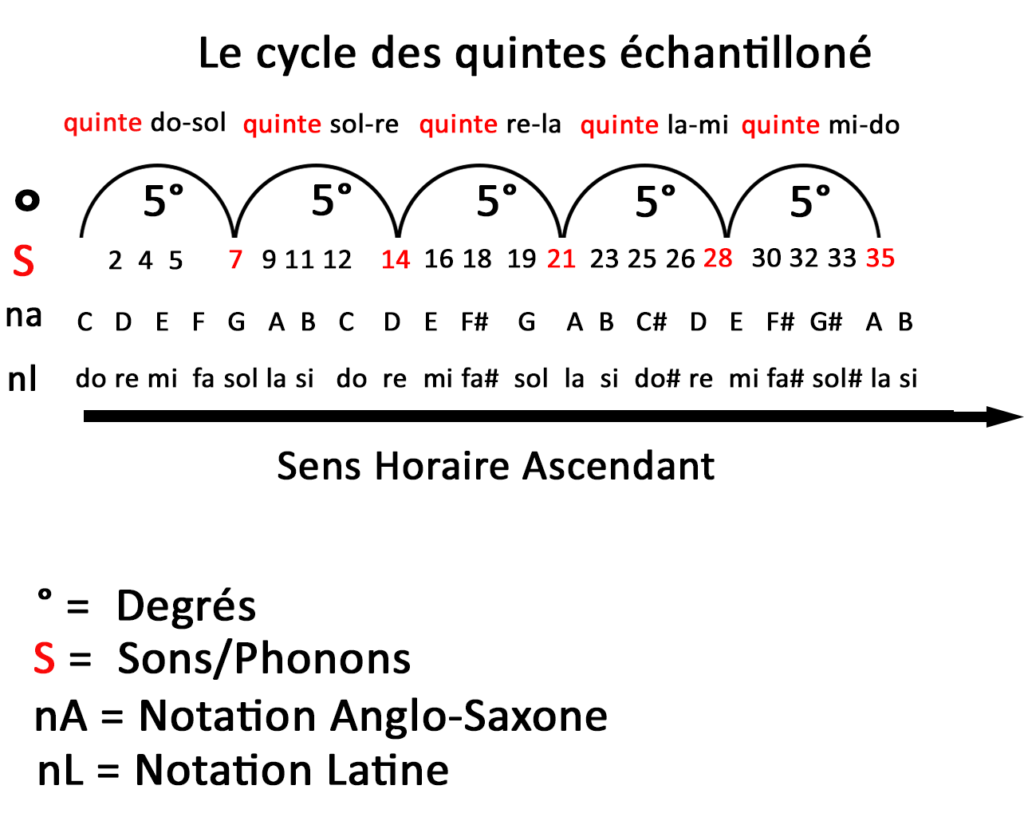
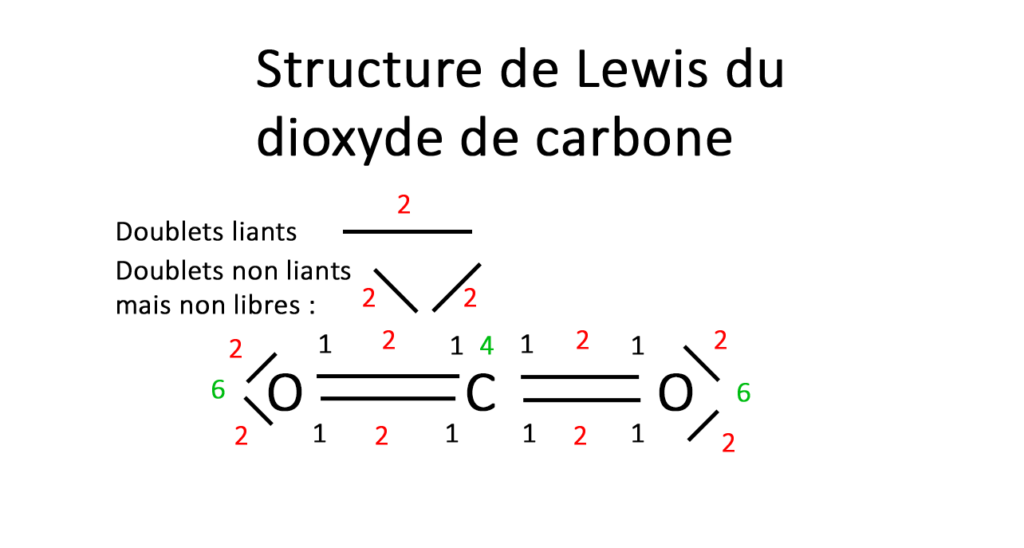
Je voulais vous faire part d’une de mes lectures c’est un petit livre synthétique de 120 pages paru fin 2022 qui résume très bien ce qu’il faut savoir sur notre consommation mondiale énergétique et électrique.
Maxence est une source et un petit génie des formes que je suis depuis quelques années, il connaît bien la doctrine défendue par Jean-Marc Jancovici. Il est diplômé de Paris Tech Chimie, a travaillé pour le commissariat en énergie atomique (CEA) en tant qu’ingénieur chargé d’affaires, il a enseigné et se spécialise sur l’énergie nucléaire.
Son livre Énergies aux éditions Tana a le mérite d’être clair et synthétique .
Il est bien présenté et riche en documentation de type diagrammes ou graphiques statistiques.
Cela m’a permis d’apprendre ou de revoir beaucoup de choses sur la nature des ressources que nous utilisons au quotidien qu’elles soient fossiles, renouvelables(photovoltaïque, éolien), bas-carbones(hydroélectrique), nucléaire(centrale électrique) ou encore thermiques (géothermie, pompe à chaleur).
Si je ne vais pas vous faire un compte-rendu de tout le livre, je vais simplement vous faire part de la première partie sur les énergies fossiles et vous résumer sommairement le reste du livre, ce sera à vous de le commander pour encourager Maxence et vous instruire pour comprendre tous les enjeux, climatiques, énergétiques, politiques qu’il dépeint.
Compte-Rendu Première partie
Dans un premier temps, Maxence explique qu’il existe 5 différentes types d’énergies : mécanique, thermique, nucléaires, électromagnétiques, chimique. En vérité certaines peuvent êtres corrélées les unes aux autres.
Il rappelle que la première source d’énergie qui conditionne toutes les autres est nucléaire, c’est celle de la fusion solaire entre hydrogène et hélium et c’est à mon sens quelque chose qu’il faut garder en tête pour notre avenir proche. (Je suis en train de lire 2 livres sur le nucléaire dont un de Maxence dont je ferai la promotion à la fin de l’article).
Si le tournant a été la révolution industrielle au 19ème siècle avec l’invention du moteur à explosion et de la machine à vapeur. Il détaille que notre énergie mondiale dépend encore aujourd’hui à 80 % d’énergies fossiles alors que nous sommes à l’ère de la transition énergétique.
D’où proviennent elles ?
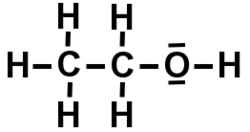
Il m’a appris un terme que je ne connaissais pas : le kérogène qui est une étape intermédiaire de la biomasse par laquelle la sédimentation des minéraux sous l’effet des bactéries se fossilise pour devenir des hydrocarbures (H et C) que l’on trouve sous la forme liquide(pétrole), gaz dit « naturel ».
De manière artificiel, on apprend que le kérogène peut être pyrolysé, (dissocié par la thermie) afin de raccourcir ses atomes de carbone et le transformer en liquide et en gaz plus rapidement.
1/Le pétrole
Maxence commence par s’intéresser au plus important des hydrocarbures, celui qui a déclenché tant de guerres injustes, d’accords commerciaux unilatéraux – l’OR noir – le pétrole.
Un baril de pétrole équivaut à 159 litres : pas un de moins, pas un de plus.
Il est issus de vieux planctons sédimentés lentement à travers la terre.
Il existe deux types de gisements principaux : les gisements dits conventionnels qui ont été exploités en majeure partie jusqu’en 2000, et les gisements de roche mère dit « schistes » de manière impropre.
Technique d’extraction et rentabilité
Ces derniers sont en majeure partie dans la mer et demandent une technique d’extraction toute particulière grâce à de l’eau pressurisée pour fracturer d’abord la roche, la maintenir ouverte avec du sable. Contrairement aux gisements dits conventionnels dont le taux d’épuisement est de 4 à 6 % ceux de roche mère sont beaucoup moins rentables et arrivent à pleine production seulement au bout d’un mois quand après 1 année ils sont déjà épuisés à près de 70 %.
Pas étonnant que les investissements diminuent d’années en années pour ce type d’extraction d’énergie fossile dont l’activité ne s’appuie plus que sur les gisements déjà préparés et prêts à être forés. Même si le pétrole est primordial, cette rentabilité est trop faible et coûteuse.
Ainsi si la demande reste croissante, le prix du baril risque d’augmenter rapidement et violemment.
Le pétrole concrètement c’est quoi ?
Il alimente la plus grande partie de nos transports, constitue la grande majorité des polymères : Le bitume de nos villes, l’asphalte des routes, tous les plastiques de nos bouteilles d’eau telles que le Polytéréphtalate d’éthylène (PET), nos claviers, nos souris d’ordinateurs, nos vêtements, nos semelles de chaussures.
Tous ça c’est ce qu’on appelle de la pétrochimie.
Les guerres du pétrole et petite géopolitique
Le pétrole a été une source de nombreux conflits pour ne citer que les guerres du Golfe en Irak ou le chaos en Syrie quand la production s’est arrêtée.
En Europe, Il faut savoir que la Russie est le principal pourvoyeur de Gaz, Charbon et Pétrole. Jusque là l’économie russe avait besoin des devises de l’UE mais sa stratégie de diversification du porte feuille tournée vers les BRICS (Brésil, Russie, Indochine, Chine, South Africa) lui permet de ne plus être dépendant de l’UE.
Le taux de retour énergétique (TRE)
Maxence insiste sur un indicateur très important le Taux de retour énergétique c’est à dire le rapport entre l’énergie que l’on récupère et l’énergie qu’il a fallu investir pour aller chercher cette énergie. (En d’autre termes il s’agit de rentabilité énergétique et non pécuniaire même si celles-ci peuvent être liées)
On apprend que dans le désert saoudien ce taux est de 100/1 ce qui est le meilleur ratio, aujourd’hui. A titre de comparaison, auparavant au 19ème siècle il était de 1000/1. Aujourd’hui ceux de roche mères sont de 4/1.
On tend indubitablement dans le futur vers du 1/1 ce qui n’est pas tenable.
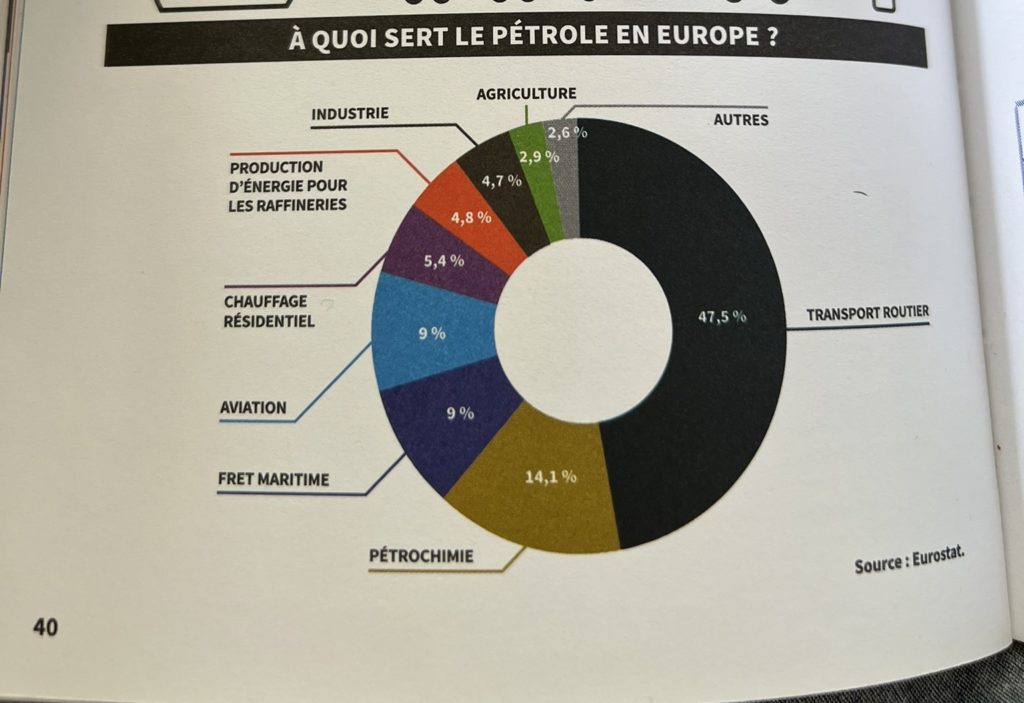
Exemple de diagramme très intéressant en rapport avec l’utilisation du pétrole en France présent dans le livre, ce n’est qu’un parmi tant d’autres.
2/ Le gaz
Le gaz CH4 (Méthane) est issu des gisements de pétrole ou le kérogène pyrolysé lentement (géothermie longue) a produit soit à la fois du pétrole et du gaz, soit uniquement du gaz si le gisement est très ancien. Donc quand on extrait du pétrole, le plus souvent on extrait aussi du gaz.
Le marché
D’abord indexé sur le prix du pétrole pour le rendre moins cher et attrayant un marché s’est peu à peu développé malgré des difficultés énormes telles que le transport (fuite) et sa faible densité (volume/énergie produite).
Son faible prix a poussé les pays a en utilisé de plus en plus et à créer des gazoducs pour l’acheminer de manière transfrontalière, en Europe (hors Russie) : la Norvège, les Pays-Bas et le Royaume-Uni en disposaient mais les gisements se sont taris et l’Europe doit de plus en plus en importer pour assurer sa survie énergétique.
Parmi ce moyen d’importation, on a le GNL ou Gaz Naturel Liquéfié, en effet le gaz peut-être cryogénisée à -161° pour être transporté par navire (États-Unis) cependant bien sûr cela demande plus d’énergie (pétrole pour le transport) et re-transformation en Gaz dans un terminal portuaire dédié.
Utilisation
En France le gaz est utilisé de manière intensive pour la production d’ammoniac afin de faire des engrais azotés pour notre agriculture mais aussi une grande source pour fabriquer de l’électricité pour chauffer.
Depuis 2010 la consommation de gaz augmente énormément parce qu’il a été bon marché par rapport au pétrole et qu’il est beaucoup moins polluant que le charbon qui rejette énormément de CO2, pourtant il reste un hydrocarbure et donc une énergie fossille.
Gaz Naturel « Clarification »
Le Gaz Naturel est appelé naturel car il est convoyé par les gazoducs, contrairement au gaz de ville et au gaz manufacturé. (Par la main de l’homme).
Ce qualificatif a été donc utilisé pour le distinguer du gaz produit dans ce qu’on appelle « une usine à gaz » ou le charbon était utilisé pour créer du gaz destiné à servir au chauffage des bâtiments et à nos éclairages publics.
Ce gaz est tout autant un combustible fossile et n’a rien d’un biogaz. Il n’a pas d’odeur ce qui est dangereux, car il est explosif et asphyxiant, alors on lui rajoute un odorisant : le mercaptan, un thiol c’est à dire un composant organique à base de souffre et plus précisément le tétrahydrothiophène.
3/ Le Charbon
Le charbon c’est quoi ?
Le charbon provient de l’accumulation de débris végétaux dans des marécages puis de leur transformation sous effet pyrolytique → tourbe → lignite → houille → anthracite.
Dans les grands gisements du Carbonifère (≈359–299 Ma), la part majeure de la biomasse venait surtout de lycopsides arborescents (ex. Lepidodendron, Sigillaria) et de prêles géantes (Calamites).
Les fougères et fougères arborescentes ont aussi contribué, mais elles ne sont pas l’unique source.
Les charbons plus récents intègrent davantage de conifères puis, encore plus tard, d’angiospermes..
Plus la peine de le présenter, le charbon est un combustible fossile fait de carbone qui peut être brun (lignite) ou noir (houille). Il a été utilisé d’abord pendant la révolution industrielle en masse.
On pense souvent que cette forme d’énergie polluante est d’un autre temps mais pourtant c’est entre les années 2000 et 2010 qu’il a le plus augmenté avec l’essor de l’économie chinoise.
Charbon local
Aujourd’hui on sait que le charbon est l’énergie la plus polluante, Maxence insiste sur la dimension locale, même si la France a fermé sa dernière usine en 2004, même les allemands continuent à l’utiliser pour ne pas dépendre uniquement de l’énergie des pétromonarchies d’Arabie saoudite, Qatar, Emirats etc.
La France malheureusement dépend beaucoup pour ses importations du charbon ainsi lorsque vous voyez une étiquette, Made In China ou Made in India c’est le plus souvent fabriqué grâce au charbon.
Résumé du reste du livre
J’ai résumé succinctement 50 pages du livre sur les énergies fossiles pour vous montrer tout son intérêt et je n’ai pas tous les diagrammes statistiques qui sont ultra-pertinents
Dans le reste du livre Maxence parle de l’électricité et notamment des énergies renouvelables, du nucléaire, d’hydro-électricité(terraformation, géomorphologie) et même de géothermie. Il enchaîne sur l’impact climatique et notamment des gaz à effet de serre présents dans notre atmosphère qui servent à retenir la chaleur en emprisonnant une partie du rayonnement infra-rouge de la planète.
Il parle de l’absorption du CO2 par nos océans ce qui les acidifie et de la manière dont nous devons tous agir pour réduire notre empreinte carbone compte tenu du fait que les énergies fossiles sont d’une part en train de se raréfier et d’autre part que leur exploitation intensive sont en train de réchauffer le climat de notre planète.
C’est clair, c’est synthétique, c’est bien écrit et bien pensé ; donc j’en fais la publicité. Je me suis procuré récemment un autre livre de Maxence qu’il a co-écrit avec Stéphane Sarrade (le directeur de chimie du CEA) et qui vient de paraître compte-tenu du fait que je pense qu’il faut vraiment approfondir pour la souveraineté de notre génération et de notre pays l’énergie nucléaire en mix avec les énergies renouvelables qu’il faut arriver à rendre pilotable 😎