Sources :
(Je me suis basé sur Je me suis basé sur le dictionnaire du CNRS, sur Wikipédia et sur un Modèle de Langage, mon Piano, d’une application mobile appelée Lambda (pour les néophytes la longueur d’onde) et d’un livre de solfège, des éditions first ah oui c’est la tour qu’on avait construite pour moi à la Défense : et qui indique la météo du lendemain🤣 dans laquelle je suis monté au sommet a 24 ans) . Petite anecdote a ce propos Même mon frère m’a fait honte : Je lui ai parlé des créateurs et quand j’ai voulu lui montrer cette tour il m’a répondu « je m’en fous de ta tour ».
J’ai une synapse spéciale qui contient 30 ans de souvenirs.
1/ Introduction lexicale
La musique a une place chère dans mon cœur. C’est un art majeur qui a un rôle très important à jouer dans notre société. C’est aussi un langage universel et une science dérivée des mathématiques..
A ce titre elle a toute sa place sur ce site pédagogique surtout quand on sait sa fonction cachée 😎.
Je souhaitais vous faire la présentation d’un théorème musical qui permet d’avoir une compréhension global d’une partie de la musique. On va l’appréhender sur le plan musical mais aussi sur le plan scientifique en parlant de fréquences, d’armure, de fractions, de gammes, de tons mais surtout de son. Tonnerre de Brest 😂.
Il s’agit du cycle des quintes inspiré par Pythagore.
Le cycle des quintes est un outil qui permet d’organiser les gammes diatoniques (majeures et mineures) selon leurs relations harmoniques et leurs altérations. Il permet aussi de visualiser les 12 sons de la gamme chromatique, en les reliant par quintes justes.
Une gamme est une suite des notes d’un système musical donné (mode), comprises dans les limites d’une octave, séparées par des intervalles déterminés et disposées dans l’ordre des fréquences croissantes ou décroissantes.
2/La légende de Pythagore et le rapport de fréquence
Jusque là rien de très compliqué, c’est alors qu’il me faut vous parler de cette histoire : la légende raconte que Pythagore en passant devant une forge fut frappé des différents sons de marteau sur une enclume.
Il distinguait quatre sons bien distinctes, entre un marteau de masse 6, 8, 9, 12, lorsque le marteau 6 frappait et que suivait le marteau 12 les deux harmoniques étaient distante d’un octave.
On a un rapport de deux fréquences = 12/6 soit 2/1 = 2 ce qui donne une octave
Quand le marteau 6 frappait et que suivait le marteau 9 c’était une quinte rapport de fréquence de 9/6 ou 3/2 soit environ 1,5 ce qui donne une quinte
Quand le marteau 6 frappait et que suivait le marteau 8 c’était une quarte rapport de fréquence de 8/6 soit 4/3 environ 1,33 ce qui donne une quarte
Quand deux marteaux de même masse frappe on a le rapport de fréquence de 1/1 = Unisson
L’octave, la quinte, la quarte sont des intervalles dits justes et nous verrons pourquoi dans la 3ème partie de l’article.
Voici une échelle diatonique qui tente de réconcilier la gamme diatonique avec la gamme chromatique en comptant le nombre de sons possibles pour un Ton ou un demi-ton à tempérament égal.
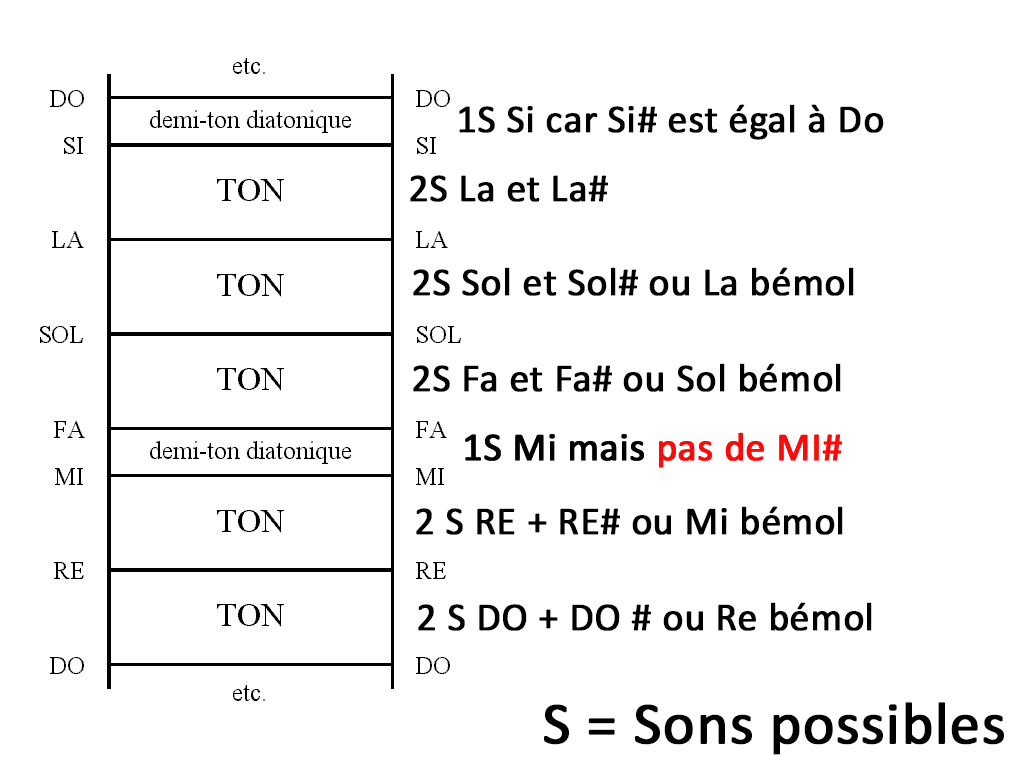
Echelle diachromatique, partez du bas dans un ton vous avez deux sons possibles à savoir le do +do # ou Re bémol jusqu’à Mi et Fa et Si et Do. Ce qu’il faut comprendre c’est que nous avons donc 12 sons possibles dans un octave 2×5+2 = 12.
Pour parler concrètement et à titre d’exemple sur un instrument tel que le piano l’écart entre une touche blanche et une touche noire consécutive correspond à un demi-ton soit 1 seul son possible : soit la valeur 1 les notes altérés correspondent aux notes noires.
L’altération d’une note c’est à dire si elle porte un symbole comme dièse va augmenter la hauteur d’un demi-ton, le bémol va la baisser d’un demi-ton. Re b(en dessous Re) = Do #(Au-dessus Do)
L’écart entre deux notes consécutives correspondent à un ton entier c’est à dire à deux sons possibles soit la valeur 2 sauf entre Mi et Fa et entre Si et Do.
Une note ne peut pas être # et bémol à la fois mais un re# est un mi bémol.
3/ Etude des intervalles
L’octave
Quand on passe au 13ème son on passe à l’octave supérieur.
Quand on joue deux sons dont la fréquence du second est le double de la première, par exemple :
- 220 Hz → 440 Hz
- 440 Hz → 880 Hz
le second son est perçu comme « le même » que le premier, mais plus aigu. Ce doublement de la fréquence correspond exactement à une octave.
Notre oreille interne et notre cerveau perçoivent les sons de façon logarithmique, pas linéaire. Cela veut dire que nous percevons une même distance musicale non pas quand les fréquences augmentent d’une même valeur, mais quand elles sont multipliées par un même facteur.
🧠 2. Perception humaine
- Une multiplication par 2 = une octave
- Une multiplication par 2×2 = 4 deux octaves
- Une multiplication par 3/2 = une quinte (ex. 440 → 660 Hz)
Cette structure logarithmique (lien direct à mon article sur les logarithme) est à la base des gammes musicales.
3. Harmoniques et consonance
Quand un instrument joue une note (fondamentale), il produit aussi des harmoniques (fréquences multiples de la fondamentale) :
- Si on joue un La à 220 Hz, ses harmoniques sont :
220,440,660,880
Le deuxième harmonique (440 Hz) est le double de la fondamentale → c’est donc une octave au-dessus.
Cette relation simple (rapport 2:1) est très consonante pour l’oreille humaine : les deux sons se superposent presque parfaitement.
Je fait un petit aparté sur cette fréquence de 440Hz qui est un diapason : Le « la4 ou la du 4ème octave. Elle représente la fréquence sur laquelle tous les instruments s’accordent et a été adopté par l’organisation internationale de standardisation(ISO) à la suite du tempérament égal.
Un petit aparté sur le tempérament égal : la physique de la musique de par sa complexité n’est pas toujours une science exacte ainsi il a fallu uniformiser les fréquences, les sons à une hauteur déterminée afin de pouvoir jouer dans la plus grande harmonie possible. Le diapason fixé à 440hz pour les trois systèmes de division de l’octave en est l’illustration parfaite.
📏 4. Notation musicale
En musique occidentale :
- Une octave est divisée en 12 demi-tons égaux (gamme tempérée)(12 sons possibles)
- Chaque demi-ton correspond à une multiplication de fréquence par la racine 12e de 2 :

La Quinte




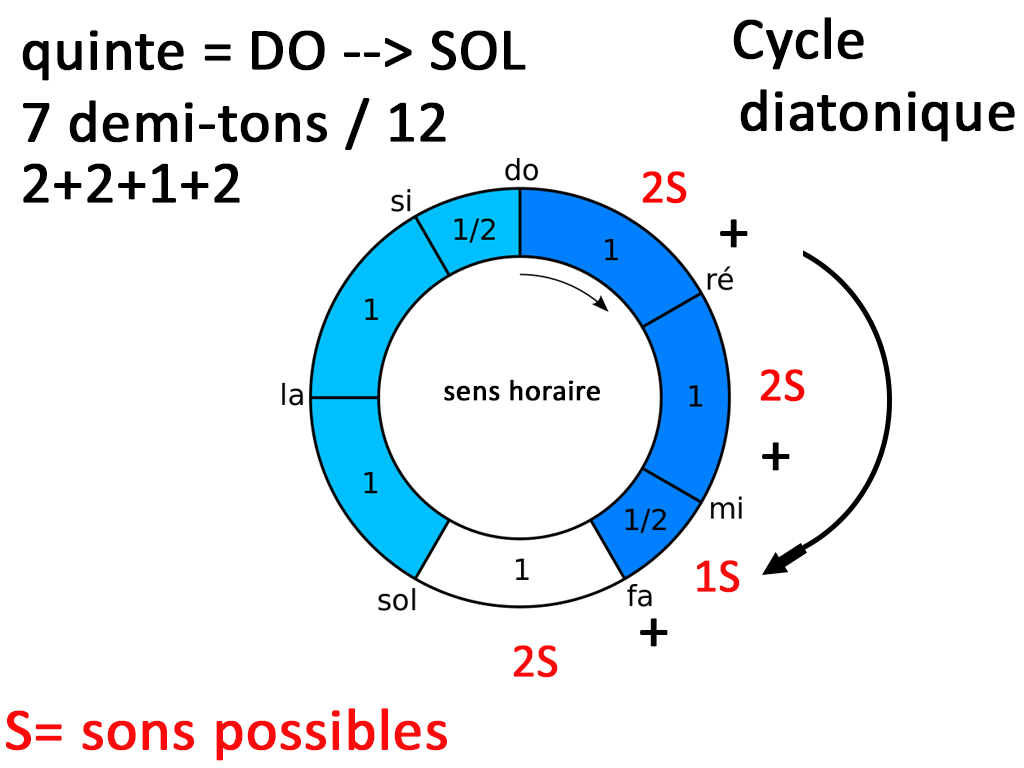
Voici un cycle diatonique que j’ai modifié pour vous montrer à quel point il est désuet. Entre Do et Sol, nous avons 5 degrés soit 5 notes donc une quinte mais 7 sons ou 7 demi-tons car 2+2+1+2 = 7. Car nous avons Do Do# ou Ré bémol, Ré, Ré# ou Mi bémol Mi Fa 1 son et Fa Fa# ou Sol Bémol 2 sons. Ce qu’il est intéressant de retenir c’est la structure 2 2 1 2 sons ou 1 1 1/2 1 ton.
On retrouve le rapport 3/2 du légendaire Pythagore
- C’est le deuxième rapport le plus simple après l’octave.
- Il est présent naturellement dans les harmoniques d’un son.
- Il est très consonant et stable pour l’oreille humaine.
- Il joue un rôle fondamental dans les gammes, les accords, et l’harmonie tonale.
La Quarte




Conclusion
Le rapport 4/3 correspond à une quarte juste car :
- Il représente une relation simple entre deux fréquences.
- Il est consonant, bien qu’un peu plus tendu que la quinte.
- Il est présent dans les harmoniques.
- Il joue un rôle fondamental dans la construction des accords et des gammes
- Il est complémentaire de la quinte dans la structure tonale. (Renversement)
4/ Le Cycle des Quintes
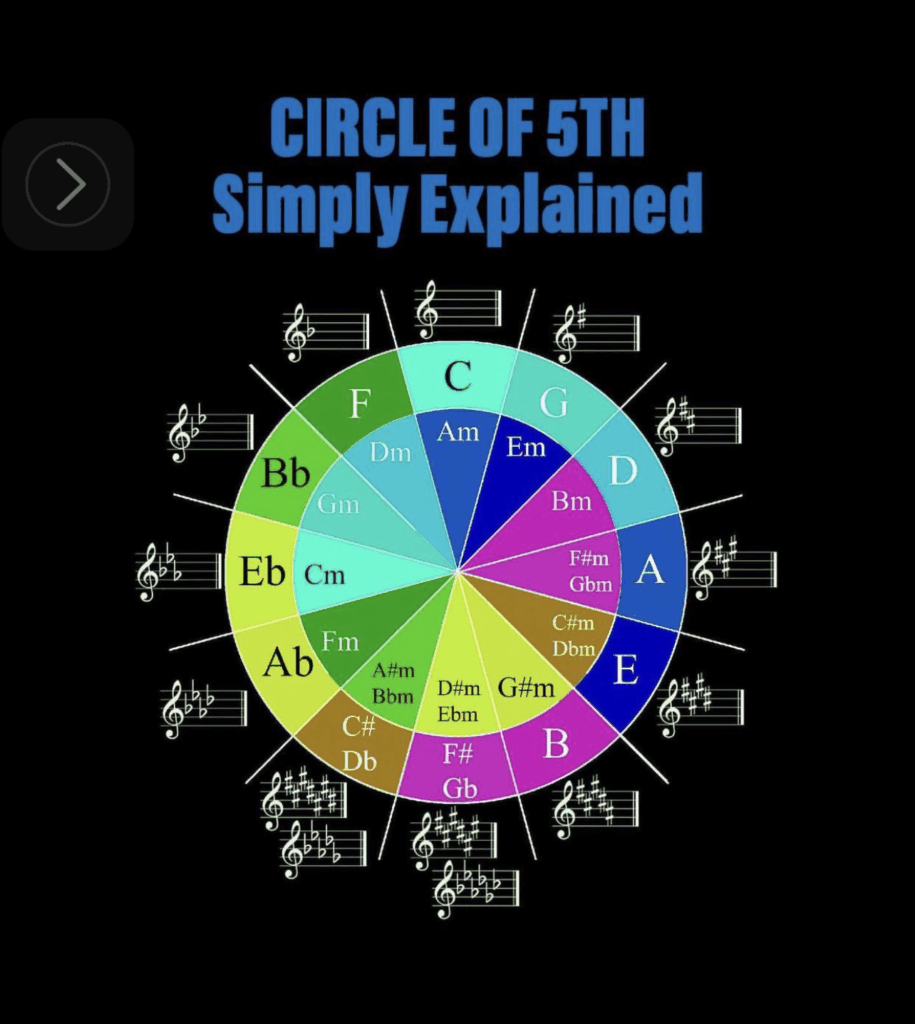
un cycle des quintes anglo-saxon sur fond noir 😊 J.C Heudin : Copyright.
Avant d’apprendre à lire le cycle des quintes il convient de comprendre toutes les notations propres aux pays anglo-saxons, aux pays latins, et germanophones.
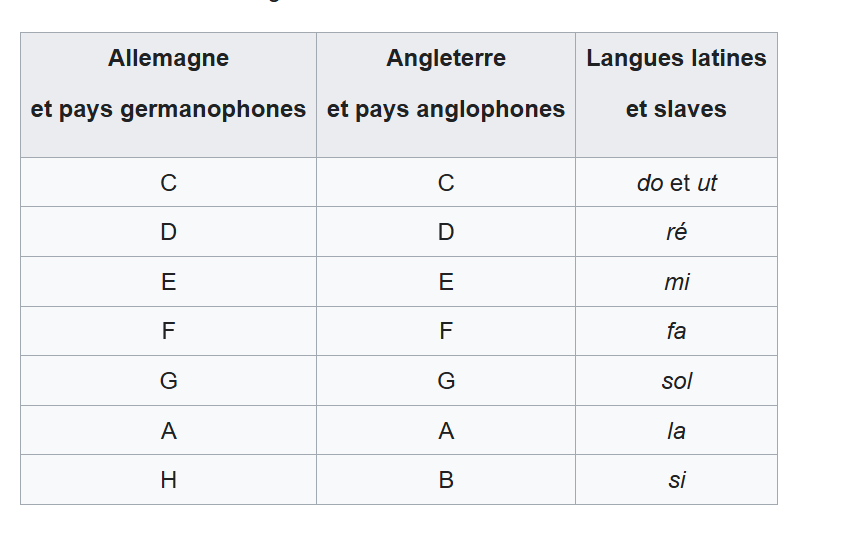
Tableau des correspondances, on pourrait presque faire correspondre avec l’hexadécimal en informatique surtout pour la notation anglo-saxonne sauf pour le G qui n’existe pas en hexa et le H (si) qui remplace le B en anglais.
Avant d’attaquer la lecture circulaire du cycle des quintes je vous ai préparé comme si vous étiez des enfants un spectre ou un échantillon d’un cycle des quintes sur une ligne en partant de Do Majeur.
Cet échantillon compte 35 sons soit 7 x 5 quintes puisque une quinte = 7/12 sons dans l’octave. Il vous permet d’apprendre les correspondances entre les notes latines et anglo-saxonnes tout en comprenant qu’une quinte représente cinq degrés. Il vous permet par arithmétique de repérer les tons (2 sons) et demi-tons (1 son).
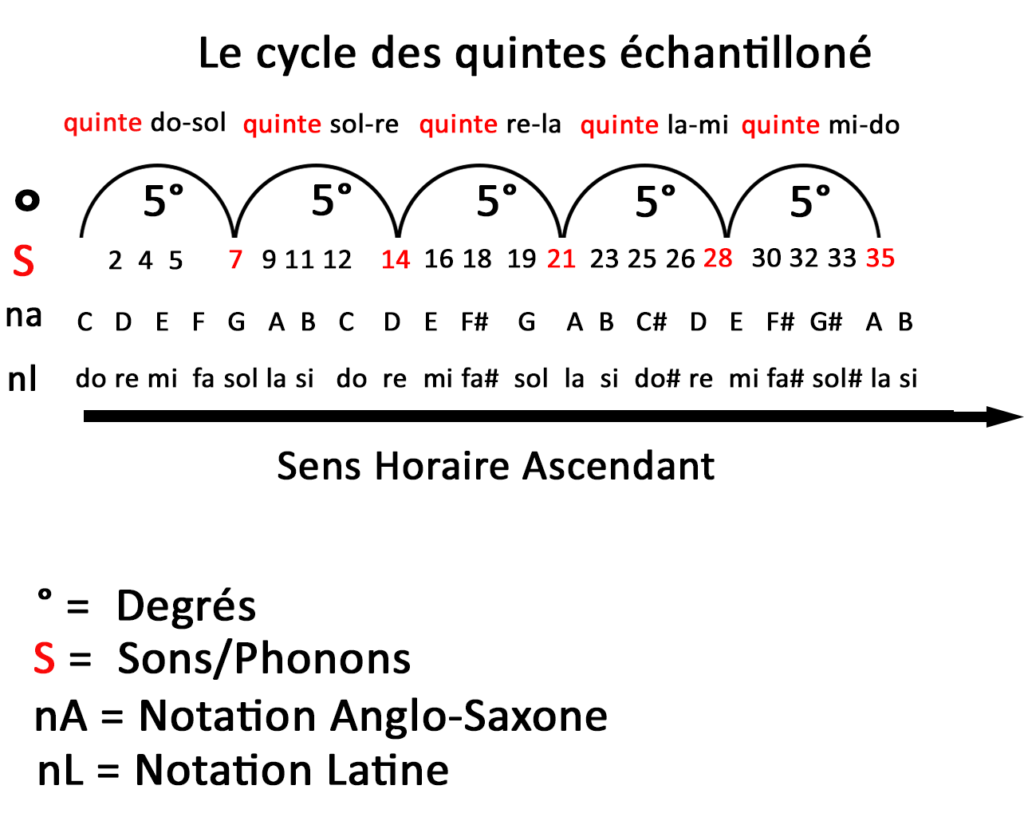
On doit respecter la structure diatonique en 2 2 1 sons ou 1 1 1/2 tons expliqué plus dans la partie sur la quinte plus haut c’est pourquoi on doit avoir un F#, (fa#) un C# (do#) un autre F# (fa#) et un G# (sol#).
Il y’a plusieurs termes qu’il convient d’expliciter pour comprendre le cycle des quintes :
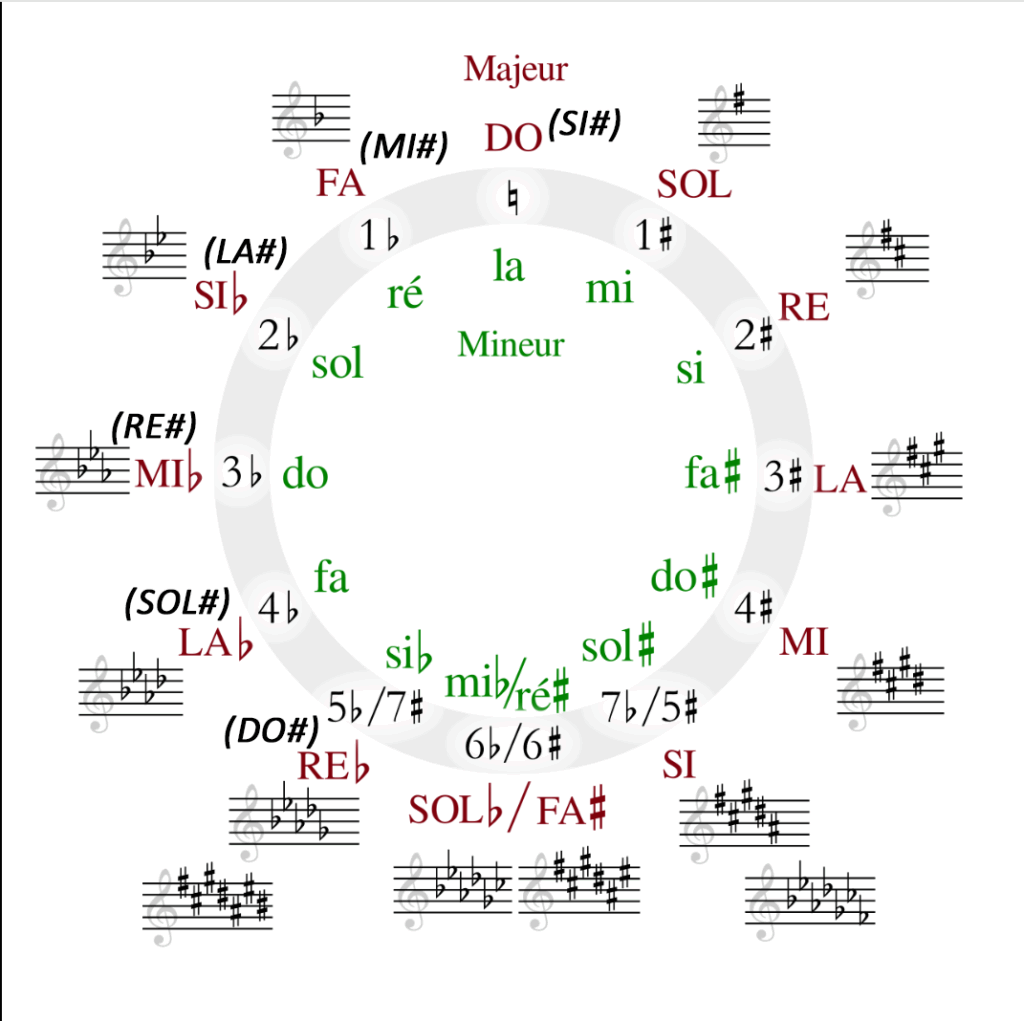
Un cycle des quintes latin sur fond blanc 😊
En haut du cercle, sont situées les gammes de do majeur et la mineur. À chaque rotation dans le sens horaire, on ajoute un dièse à l’armure, selon le cycle des quintes ascendantes, soit dans l’ordre : fa, do, sol, ré, la, mi, si. Dans le sens antihoraire on ajoute un bémol à l’armure et on procède par quartes, descendantes, ce qui donne : si, mi, la, ré, sol, do, fa. Le nom des gammes correspondantes suit également ces deux ordres. Enfin la quarte et la quinte se retrouvent en SOL bémol/ FA # à la moitié du cycle de 12 quintes à 6 ce qui confirme que quinte et quartes forment bien un octave soit 12 sons et sont complémentaires.
Un petit point lexicologique s’impose :
enharmonie : les notes qui se superposent comme mi bémol ré# ou fa# sol bémol sont des notes enharmoniques. Ce sont deux notes qui obéissent à des procédés harmoniques et qui sont distantes d’un comma.
L’armure :
L’armure c’est la réunion à la clef de toutes les notes qui vont être altérées sur la portée. C’est la petite portée que vous voyez en dessous de la note avec les dièses et les bémols.
Ensemble des caractères liés au choix d’une tonique déterminée (en vert sur le cycle des quintes latin) Elle peut-être majeure ou mineure. Rien n’empêche une tonalité d’être modulé dans un opus.
Première note d’une gamme. Elle donne son nom à cette gamme et au ton de cette gamme. Par exemple, on dit: la gamme et le ton d’ut (do), qui est la tonique.
Petit exemple :
Lorsque je parle de la Sonate au clair de Lune de Beethoven je parle de la sonate opus(lat. oeuvre) n°14 (est la référence dans le catalogue de l’auteur). C–Sharp.
C veut dire Do qui est la tonique et Sharp veut dire dièse : c’est une tonalité Mineure. Tout ce qui est au bémol en anglais flat ou encore ce qui est sans altération comme le ton ut (do) est une tonalité Majeur, on a trois mouvement comme souvent dans les symphonies, sonates et concertos et le rythme (tempo) est indiqué en italien.
Dans la Sonate au clair de lune la tonalité est modulé plusieurs fois en fonction des mouvements et des passages telle la modulation de fréquence du chant d’un oiseau(Nature) ou les modulations des impulsions électriques d’un routeur internet.(Physique) ou l’arithmétique modulaire utilisé en cryptanalyse(Mathématiques).
Mathématico-musicalement, Pythagore avait établi un cycle des quintes qui illustrait ses théories. Mais la précision de ses calculs était telle qu’elle n’est plus applicable de nos jours. Au bout de 12 quintes justes successives do-sol-re-la-si-fa#-do#-sol#-ré#-la#-mi# : la dernière note est très légèrement plus haute que le do initial, alors que sur le piano les deux notes sont les mêmes. Même si la différence est vraiment minime, pour être précis, elle est de 531441/524288 soit
1,01364326477051.
Cette valeur dépend de la vibration du matériau qu’a utilisé Pythagore pour fonder ses calculs, il n’a pu calculer dans l’abstraction pure sans mesurer par son sens auditif comme l’illustre l’apologue du marteau du forgeron. Il est fort probable que les atomes du matériau qu’il a écouté pour effectuer ses calculs soient différents de ceux d’une corde frappée d’un piano.
On en revient au tableau périodique, il faudrait étudier les phonons (Température de Debye) c’est à dire les vibrations atomiques et leurs accumulations précédentes successives dans la configuration spatiale cristalline et leurs diffusions (séries de notes ou quintes précédentes) de chaque élément (oxygène,instruments à vent, cuivres),(cordes frottées(boyaux de moutons chaleur plus forte du au frottement) ou frappées (métal, acier, piano bref ), pour essayer de retrouver cette différence entre le si# et le do.
Voilà je pense que vous pouvez vous entrainer à comprendre ces cycles avec une simple feuille de papier en écrivant do ré mi fa sol la si do plusieurs fois à la suite comme le chantait mon professeur de musique au collège..
1/2 ton = 1 son, 1 ton = 2 sons (2 fréquences). Vous pouvez vous aider d’une échelle chromatique ou d’un instrument comme un clavier virtuel ou réel (piano, synthé…).



