Je suis heureux de vous apprendre que j’ai commencé à me former sur LATEX (lire l’article précédent) et que c’est facile et puissant. Les images des équations intégrées à cet article ont été formalisés grâce à cet outil.
D’ailleurs le meilleur site pour se former en ligne qui dispose d’un compilateur en temps réel : https://overleaf.com/
Je vous conseille de lire en préambule l’article précédent sur les systèmes numériques : vous comprendrez mieux l’utilité de la fonction logarithme.
Passons aux choses sérieuses :
Littéralement, la fonction logarithme est le nombre de puissances que contient un nombre calculé en fonction d’un autre nombre appelé base.
Prenons un nombre voisin du nombre de ports que l’on peut ouvrir sur un ordinateur : 65535
Par un rapide calcul mental :
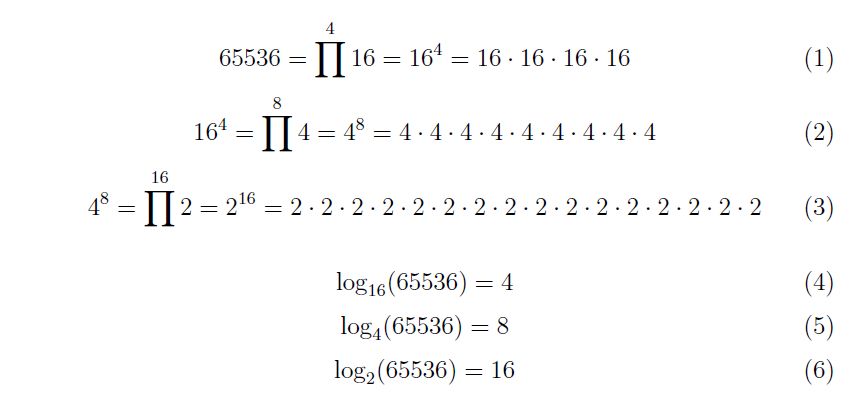
En effet 65536 est divisible par 4 car ses deux derniers chiffres forment 36 qui se décompose en 9 fois 4. Si il est divisible par 4 il est donc divisible par 2, on aurait pu s’en douter le nombre de ports d’un ordinateur étant codé en binaire ! Ainsi on calcule facilement le logarithme.
Réalisons maintenant à partir de ces résultats une simple équation logarithmique :
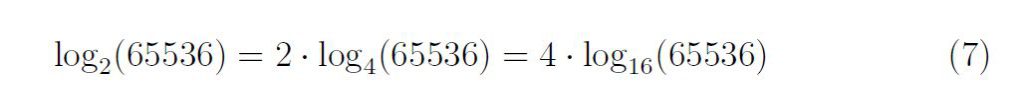
Voici des équations en passant par trois bases différentes de la base 2 à la base 4, à la base 16.
On change facilement de base dans cet exemple car on passe d’un carré à un carré, le résultat d’un logarithme étant basé sur une fonction puissance ce serait plus difficile de faire une équation en changeant la base vers une base multiple comme 32. Pour réaliser l’égalité on juste placé un coefficient devant la fonction en l’occurrence 2 et 4.
Maintenant, entrainons nous :
Alors quel est le prochain carré ? Et quelle équation allons nous devoir réaliser ?
Oui 256 est le carré de 16 !
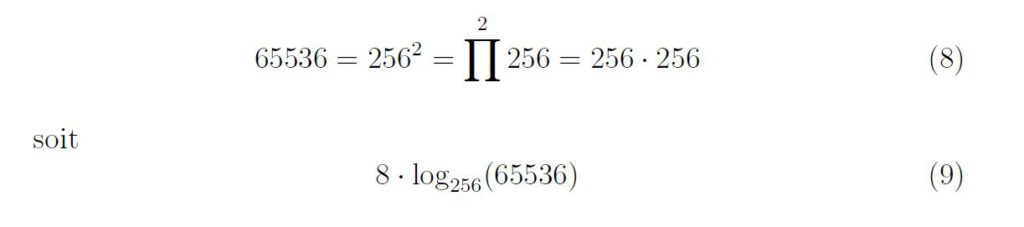
Simple non ?
Par contre diviser 65536 par 10 ne donnerait pas un entier naturel mais un nombre avec une partie décimale ou à virgule flottante.
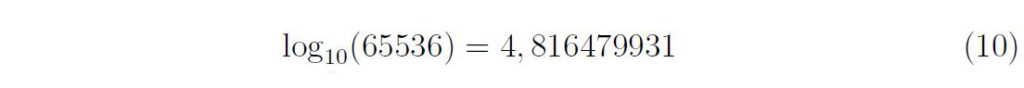
Même si il y’a trois bases remarquables (les plus fonctionnelles) qui sont la base de 10, la base de 2 noté lb (binaire) et la base naturelle qui utilise le nombre exponentiel il y’a en réalité autant de bases qu’il y’a de nombres dans notre système numérique.
Autre exemple avec un log de base 10 de 255 :
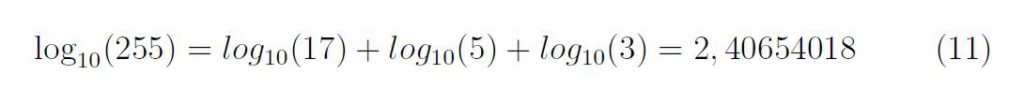
Notez que si on multiplie les logarithmes de base 10 des nombres additionnées entre eux on obtient 17x5x3=255 qui est le nombre dont on souhaitait calculer le logarithme au départ.
Pourquoi c’est utile en informatique ? Le code machine est dans un système binaire donc sur une base 2 :
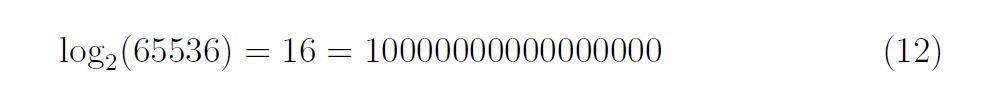
Sur un encodage positionnel, en binaire, (sur une base 2) le résultat du logarithme donne le nombre de 0 soit 16 avant le premier bit encodé donc sur le 3ème octet.
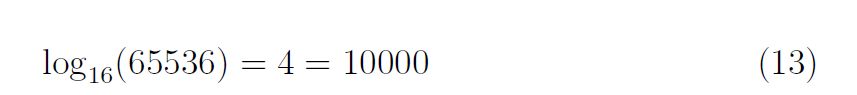
En hexadécimal (sur une base 16) le résultat du logarithme donne le nombre de 0 soit 4 avant le premier bit encodé également sur le 3ème octet. En hexadécimal car 16 (base) /8 (nombre de bits dans un octet) = 2 donc un octet est encodé sur 2 valeurs.
Bien sûr, vous pouvez aller plus loin et par exemple comprendre la formule pour le changement de base pour une équivalence non carrée qui est à mon avis une clé pour jongler entre les systèmes !
Pour ceux qui veulent télécharger tout le document au format .pdf compilé par LATEX pour voir à quoi ressemble une publication scientifique, c’est là : Logarithme
Pour ceux qui veulent le code source du document LATEX à titre pédagogique pour connaître le nom de certaines balise, c’est là : Code Source



