Lorsque l’on me demande ce qu’il faut apprendre en premier lieu en informatique, je répondrai sans hésiter les systèmes numériques et essentiellement le binaire. Vous savez cette suite de 0 et de 1 traduction du langage maternel de la machine dérivés des mathématiques et de la physique.
Ce langage est celui que comprend et utilise le processeur pour fonctionner au plus bas niveau. Son inventeur Claude Shannon (inventeur de la théorie de l’information) l’a utilisé en électronique et en informatique pour représenter l’information d’une impulsion électrique qui passe « 1 » ou ne passe pas « 0 ».
Shannon ayant travaillé lors de sa thèse sur l’algèbre de Boole basé déjà sur des variables à deux états VRAI OU FAUX, les suites de bits « binary digit » que sont 1 ou 0 ont permis un meilleur contrôle du signal électronique et sa numérisation. Ces suites, ont été appliqués, interprétés et encodés via d’autres tables ou schémas.
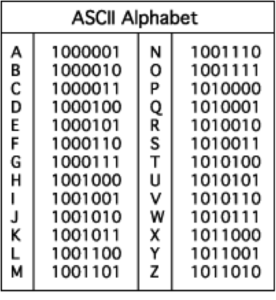
Par exemple pour représenter l’alphabet par exemple la fameuse table ASCII « American Standard Code for Information Interchange » qui comprend 128 caractères et notamment les 26 lettres de l’alphabet encodés sur une suite de 7 bits.
Comprendre le binaire c’est savoir le transformer dans d’autres systèmes numériques, j’ai nommé le système décimal basé sur 10 chiffres : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Ou encore de plus en plus répandu même si moins familier le système hexadécimal voir octal (permissions Linux).
Par curiosité ou si vous êtes intéressé par une carrière d’administrateur réseau, vous devrez jongler pour calculer vos masques avec au moins deux systèmes : décimal et binaire.
Bien sûr, il existe pléthore de petits logiciels, calculatrices qui feront la conversion pour vous, mais c’est important de comprendre la mécanique derrière ces séries de nombres.
Dans le cas d’une adresse IP par exemple, on a utilisé le système décimal pour représenter l’adresse bien que cela soit des bits. Une adresse IPv4 est encodé sur 32 bits soit 4 fois 8 bits. Ainsi lorsque que vous voyez 192.168.0.100 c’est en fait 32 1 ou 0 que vous avez en fait.
Mais alors comment passer du système décimal au système binaire ? En fait le système binaire est basé sur des mathématiques et plus précisément des puissances de 2. Cette puissance est positionnelle et croissante en fonction de la place du bit dans un sens de lecture de droite à gauche.
Prenons un exemple : 192 le premier terme de notre adresse est codé sur 8 bits mais comment transformer 192 en binaire ?
192 = 01100000
Comment ai-je fait ?
Connaissez vos puissances de 2 ! Tous les informaticiens connaissent leurs puissances de 2 au moins jusqu’à 4096 et sont ainsi habitués à jongler notamment avec d’autres concepts mathématiques : logarithme (base 2)
Dans l’exemple : 192 = 01100000 en commençant par la droite on a alors 0x2^0 = 0 puis 0x2^1 et ainsi de suite pour arriver aux bits qui nous intéressent et qui sont eux en état « on » ou « allumés » c’est-à-dire à l’état « 1 » : 1×2^5 et 1×2^6 qui valent respectivement en système décimal : 128 et 64.
Au final vous faites la somme de 128 et 64 vous obtenez 192 ! Alors pas si compliqué ?
Attendez en 1956 vient la création du langage hexadécimal très répandu parmi les électroniciens et qu’on est de plus en plus amené à voir :

On a décidé ainsi de rajouter 6 nombres aux 10 chiffres arabes que l’on connaît : ceux si sont représentés par des lettres :
- A = 10
- B = 11
- C = 12
- D = 13
- E = 14
- F = 15
Pourquoi ? Sûrement pour gagner de la place, faciliter la lecture, et gagner en grandeur ! En effet on a plus 10 chiffres avec le 0 mais 16 nombres avec le 0 : Ainsi on ne se basera plus sur des puissances de deux mais de 16 !
Le système pour calculer est le même bien que l’on connaisse moins de puissance de 16 que de puissance de 2.
Exemple :
A2C8 = 41672
Le principe est le même en partant de la droite :
8×16^0 = 8 x 1 = 8
C= 12×16^1 = 192
2 x 16^2 = 512
A = 10×16^3 = 40960
= 40960 + 512 + 192 + 8
= 41672.
Vous avez compris ? Entrainez vous avec des petits nombres sur un tableur excel : Toutes les fonctions des systèmes numériques binaires, hexa et décimal ont été codé et vous permettent de passer de l’une à l’autre facilement.
